Goals

To better learn about how breadth first search works by implementing it.

Logistics

This is a lab assignment that you’ll be handing in on Moodle. You should complete it on Wednesday Feb 3rd, but it isn’t due until Friday Feb 5th at 5:00pm Central.

Open the BFS Lab on Repl.it.

You’re welcome to work on this lab with input from one or more members of your collaborative learning group. You should write all of your own code, but you’re welcome to share your screen/use multiplayer mode with members of your collaborative learning group to look at one another’s code, make suggestions, and compare ideas. Take a look at the Collaboration Policies document on Moodle if you have any questions about what’s permitted.

Exercise 0

Using the Add File button on repl.it, add a Collaborations.txt file and describe any interactions you have with your collaborative learning group on this lab. Also note any outside sources such as websites that you referenced.

Exercise 1

This lab uses a provided implementation of an unweighted graph: MysteryUnweightedGraphImplementation that is the same as you will use for the homework.

a. View the JavaDocs for the graph implementation.

b. In the main function of Main.java, create an undirected UnweightedGraph with 4 vertices:

UnweightedGraph example = new MysteryUnweightedGraphImplementation(false, 4);

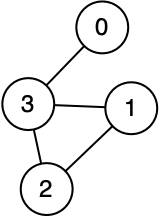
c. Add edges between vertices to achieve this graph: Undirected graph with edge between node 0 and 3, node 3 and 1, node 3 and 2, and node 1 and 2

d. Print the number of edges of the graph to verify that you created all four.

Exercise 2

You’re now ready to implement breadth first search.

a. You’ll need to reference the JavaDocs for Map and Queue, open them now:

b. Create a HashMap that contains Integer keys and Integer values to store the shortest path length from the start vertex to each other vertex in the graph.

c. The distance from the start vertex to itself is 0 so put that information into your Map of path lengths.

d. We want a Queue to keep track of which vertices we’ve seen and which vertex we need to explore next during BFS and in Java, LinkedList implements the Queue interface, so create a linked queue to store the vertex numbers:

Queue<Integer> myQueue = new LinkedList<Integer>();

e. Put the start vertex into the queue. Make sure your code compiles.

Exercise 3

Now you’re all set to implement the while loop of BFS. Implement the following algorithm:

a. While the queue isn’t empty

b. Grab the vertex from the front of the queue

c. For each of its neighbors

d. If the neighbor hasn’t been visited (hint: a visited neighbor will have a recorded path length already)

e. The shortest path distance to the neighbor is the distance to the current vertex plus one

f. Add the neighbor to the queue. The neighbor is now considered visited, but not explored.

g. Once all the neighbors are visited, this current vertex is considered fully explored and removed from the queue.

Once the queue is empty, all vertices that are accessible from the start vertex have been found and their shortest path length identified.

Exercise 4

Check that your algorithm is able to correctly identify the shortest path length between each of the following vertices:

a. 0 to 3

b. 0 to 1

c. 0 to 2

d. 1 to 3

e. 2 to 0

Exercise 5

Create another more complicated graph and verify your algorithm works on it as well. In particular, see what your algorithm does on a graph where some vertices aren’t accessible from the start vertex.

Submitting

This activity is not a homework assignment. That means that you’re evaluated on whether you attempted all parts of it, but your work will not be graded for correctness as long as a clear effort has been made. If you aren’t able to complete some parts, great ways to indicate clear effort are to reach out for help before the deadline (note ways you did so in your Collaborations.txt file) and to use comments in the document to indicate things you tried but what went wrong/where you got stuck. Feedback on labs and activities is less detailed than on homework.

Submit your zip file to Moodle as always.

Extensions

After you’ve submitted the lab, you can further challenge yourself by:

  • Creating a directed graph and trying out your algorithm
  • Extending your algorithm so that it returns the actual path, not just the length of the path