Traversals Lab

Goals

To implement and analyze breadth-first traversal (and possible depth-first as well).

Logistics

This is a lab assignment and so you will not be submitting it. However, the concepts and practice will help you on both the homework and quizzes so I encourage you to make a serious effort on it during class and consider finishing it outside of class.

I recommend making a folder for today’s lab in COURSES as you usually do.

Exercise 1

We’re going to implement breadth-first traversal based on this pseudocode:

Algorithm getBreadthFirstTraversal(originVertex) {
   traversalOrder = a new queue for the resulting traversal order
   vertexQueue = a new queue to hold vertices as they are visited
   Mark originVertex as visited
   traversalOrder.enqueue(originVertex)
   vertexQueue.enqueue(originVertex)
   while vertexQueue isn't empty
   {
      frontVertex = vertexQueue.dequeue()
      for each neighbor of frontVertex
      {
         nextNeighbor = next neighbor of frontVertex
         if (nextNeighbor is not visited)
         {
            Mark nextNeighbor as visited
            traversalOrder.enqueue(nextNeighbor)
            vertexQueue.enqueue(nextNeighbor)
         }
      }
   }
   return traversalOrder
}

Here is starter code and the associated JavaDocs for a graph implementation. In Main.java I’ve provided code to create this graph:

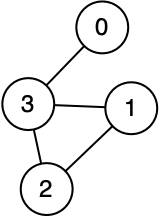
Implement breadth first traversal based on the pseudocode above (I recommend copying the pseudocode into VSCode as comments to guide you). You can use the getNeighbors graph method like so:

for(Integer neighbor : inputGraph.getNeighbors(frontVertex)) {
    ...
}

Here are the JavaDocs for Map and Queue:

• Queue interface
• Map interface

You’ll probably want to use a map to store if a vertex is visited for the sake of efficiency.

Note: make sure both partners have this code, it will be quite helpful for the homework. Feel free to adapt it for the homework, but cite your lab partner if you do so.

Exercise 2

Now let’s think about the time complexity of breadth-first traversal (or breadth-first search in the worst case). When we analyze the time and space complexity of graph algorithms, the convention is to use |V| for the number of vertices/nodes in the graph and |E| for the number of edges in the graph. Because the complexity of graphs often depends on both the number of vertices and the number of edges, you’ll often need to express the complexity in terms of |V| and |E|.

a. Analyze the number of simple operations that are required at each step of the above algorithm and note them on your worksheet

b. Some of the lines of pseudocode are hiding a fair amount of detail, such as for each neighbor of frontVertex and nextNeighbor = next neighbor of frontVertex. What assumptions are you making about the implementation details and efficiency of those lines? What could lead to those lines being more/less efficient?

c. Based on your step-by-step analysis, provide a function that describes the worst-case time complexity of the algorithm using only V. This function should include the constants and coefficients.

d. What is the Big-O time complexity of BFS in terms of V?

e. This is actually an over-estimate for most graphs. If you were going to use E as well, how could you make your time complexity potentially more accurate for sparse graphs?

Challenge Problem

Depth-first traversal is much more difficult to analyze the time complexity, but here is some pseudocode, give it a shot! (Or feel free to just try to implement it instead if you prefer):

Algorithm getDepthFirstTraversal(originVertex) {
   traversalOrder = a new queue for the resulting traversal order
   vertexStack = a new stack to hold vertices as they are visited
   Mark originVertex as visited
   traversalOrder.enqueue(originVertex)
   vertexStack.push(originVertex)
   while (!vertexStack.isEmpty()) //hint, this is the tricky part, 
                                 //how many times will this loop?? More than V!
   {
      topVertex = vertexStack.peek()
      if (topVertex has an unvisited neighbor)
      {
         nextNeighbor = next unvisited neighbor of topVertex
         Mark nextNeighbor as visited
         traversalOrder.enqueue(nextNeighbor)
         vertexStack.push(nextNeighbor)
      }
      else // All neighbors are visited
         vertexStack.pop()
   }
   return traversalOrder
}

Extra

If you have more time, try these:

1. The algorithm given in homework 3 (the maze solver) is a specialized version of depth-first search. Analyze it and determine what it’s time complexity is; why is it different than general depth-first search?
2. Implement depth-first search as well.