Traversals Lab

Goals

To implement and analyze breadth-first traversal (and possible depth-first as well).

I recommend making a folder for today’s lab in COURSES as you usually do.

Exercise 1

First let’s think about the time complexity of breadth-first traversal (or breadth-first search in the worst case). Here is some pseudocode:

Algorithm getBreadthFirstTraversal(originVertex) {
   traversalOrder = a new queue for the resulting traversal order
   vertexQueue = a new queue to hold vertices as they are visited
   Mark originVertex as visited
   add originVertex to traversalOrder
   add originVertex to vertexQueue
   while vertexQueue isn't empty
   {
      remove frontVertex from vertexQueue
      for each neighbor of frontVertex
      {
         if (neighbor is not visited)
         {
            Mark neighbor as visited
            add neighbor to traversalOrder
            add neighbor to vertexQueue
         }
      }
   }
   return traversalOrder
}

Remember that when we analyze the time and space complexity of graph algorithms, the convention is to use |V| for the number of vertices/nodes in the graph and |E| for the number of edges in the graph. Because the complexity of graphs often depends on both the number of vertices and the number of edges, you’ll often need to express the complexity in terms of |V| and |E|.

a. Analyze the number of simple operations that are required at each step of the above algorithm and note them on your worksheet

b. Some of the lines of pseudocode are hiding a fair amount of detail, such as for each neighbor of frontVertex. What assumptions are you making about the implementation details and efficiency of those lines? What could lead to those lines being more/less efficient?

c. Based on your step-by-step analysis, provide a function that describes the worst-case time complexity of the algorithm using only V. This function should include the constants and coefficients.

d. What is the Big-O time complexity of BFS in terms of V?

e. This is actually an over-estimate for most graphs. If you were going to use E as well, how could you make your time complexity potentially more accurate for sparse graphs?

Exercise 2

Now try out implementing breadth-first traversal using the pseudocode above.

Here is starter code and the associated documentation for a graph implementation. In Main.kt I’ve provided code to create this graph:

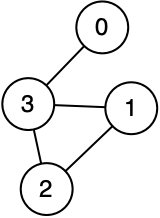
Implement breadth first traversal based on the pseudocode above (I recommend copying the pseudocode into VSCode as comments to guide you). You can use the getNeighbors graph method like so:

for(neighbor in inputGraph.getNeighbors(frontVertex)) {
    //...
}

Challenge Problem

Depth-first traversal is much more difficult to analyze the time complexity, but here is some pseudocode, give it a shot! (Or feel free to just try to implement it instead if you prefer):

Algorithm getDepthFirstTraversal(originVertex) {
   traversalOrder = a new queue for the resulting traversal order
   vertexStack = a new stack to hold vertices as they are visited
   Mark originVertex as visited
   add originVertex to traversalOrder
   add originVertex to vertexStack
   while vertexStack isn't empty //hint, this is the tricky part, 
                                 //how many times will this loop?? More than V!
   {
      if the topVertex has an unvisited neighbor
      {
         add unvisitedNeighbor to traversal order
         add unvisitedNeighbor to the stack
         Mark unvisitedNeighbor as visited
      }
      else // All neighbors are visited
         remove topVertex from the stack
   }
   return traversalOrder
}

Extra

If you have more time, try these:

1. The algorithm given in homework 3 (the maze solver) is a specialized version of depth-first search. Analyze it and determine what it’s time complexity is; why is it different than general depth-first search?
2. Implement depth-first search as well.