Analysis Lab
Goals
To get a better understanding of how to calculate the efficiency of algorithms - developing both your ability to work through calculations mathematically and your intuitive sense of estimating big-O
Logistics
This is a lab assignment that you’ll be handing in on Moodle. You should complete it on Monday Oct 4th, but it isn’t due until Wednesday Oct 6th at 5:00pm Central.
There is no coding in this assignment, so you will submit a PDF of your solutions. You have several options for how to produce this PDF:
- Write it by hand and scan it into a PDF. If you do this, you must write very neatly and clearly. Make sure to check that your scan is completely legible!
- Write it in a word processing program, then export or print it to PDF.
- Write it in LaTeX and typeset it as a PDF. LaTeX is complicated to use at first but allows you to format math very nicely. Overleaf.com is a nice website to use for writing LaTeX.
I recommend just using a word processing program and exporting/printing to PDF!
You should work on this with your in-class partner, but you both need to submit separately and therefore, if you are writing on paper, you both need to be writing your own copies. If you finish it outside of class without your partner, note which sections you completed together and which you completed separately in your Collaborations section.
Exercise 0
Create a Collaborations section of your document and describe any people you get help from on this lab. Also note any outside sources such as websites that you referenced.
Exercise 1
For each of the code snippets below answer the following:
1) How many times is the output statement printed? Your answer should be in terms of n.
2) How does the number of times the statement is printed grow with the size of n, in big-O notation? Write the tightest bound you can (e.g., if the statement is printed O(n) times, saying it’s printed O(n500) times will not be considered correct here, even though it’s technically accurate).
a.
for (int i=0; i < 2*n; i++) {
for (int j=0; j < n; j++) {
System.out.println(i + " " + j);
}
}
b.
for (int i=0; i < n; i++) {
for (int j=0; j < 5; j++) {
System.out.println(i + " " + j);
}
}
c.
for (int i=0; i < 7*n; i++) {
System.out.println(i);
}
for (int j=0; j < n; j++) {
System.out.println(j);
}
Exercise 2
Now we will use the definition of big-O to show the asymptotic order of an algorithm. Remember that these still aren’t formal proofs, we’re just aiming to find values of a C and an n0 that work and demonstrate that they work (by showing the calculation). (n0 is what the book called N, I just prefer n0.)
For this exercise, you will show that (1/5)n+30 is in O(n) by finding a C and an n0 that demonstrates this property.
(If you already have a strategy for how to find a C and an n0 that demonstrates this, you are welcome to use that and show the calculation that verifies your values. If you aren’t sure how to find the values, walk through the parts of this exercise.)
a. A good starting place is to try n0 = 1 and try to find a C that works. We want to find a C such that our function is less than or equal to C*n for all n greater than or equal to n0 which we’ve started with as 1. Write down that mathematical expression.
Show solution
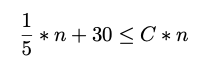 For all n >= 1.
For all n >= 1.
b. When solving for a specific variable, we always want to try to get that variable on one side of the inequality sign, so divide both sides by n.
Show solution
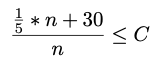
c. We now need to figure out how to get n out of our expression. Because we are dealing with an inequality, we can change the value on one side as long as we are respecting the rules of the inequality. How can you change the expression so that you can eventually factor out n as long as n >= 1?
Show solution
Because this is an inequality that we are trying to show, you can increase what is on the smaller side because it will still prove that (1/5)n +30 <= Cn
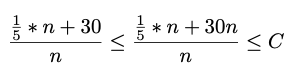
d. Now factor out n so that you are left with a value for C.
Show solution
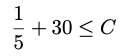
e. Report your n0 and C values that show that (1/5)n+30 is in O(n) by writing: “Thus if C = ?? and n0 = ??, then Cn >= (1/5)n+30 for all n>=n0, so by the definition of big-O, (1/5)n+30 is in O(n).”
Show solution
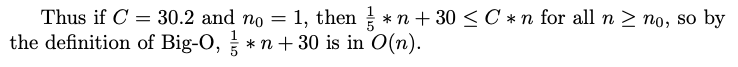
Exercise 3
Now you’ll follow the same steps as in Exercise 2 to show that 7n3+2n is O(2n).
a. Repeat steps a and b from Exercise 2 for the new expression (you won’t be dividing by n this time).
b. We want to do something similar to 2c to deal with the n3 term. However we have to respect the inequality and substitute something larger. Is 2n larger than n3 when n is 1? What about when n is 2?
c. Even though the expressions are equal when n is 1, we need to respect the inequality for all n larger than n0 so you should always check a couple of larger values when doing substitutions. We have to change our n0 so that we can make the substitution. Try out larger values of n until you find one where for it and all values larger than it, 2n is larger than n3. You could use software to plot both functions and find where they intersect, but for this exercise, you can probably just try a few values.
d. With our new n0, we know that 2n will always be larger than n3 and so can make the substitution in our expression.
e. Simplify your expression until you have a value for C and report your values the same as in 2e.
Exercise 4
The same as in Exercises 2 and 3, show that 8n2 + 3n is in O(n3) (not a typo!).
Submitting
This lab is not a homework assignment. That means that you’re evaluated on whether you attempted all parts of it, but your work will not be graded for correctness as long as a clear effort has been made. If you aren’t able to complete some parts, great ways to indicate clear effort are to reach out for help before the deadline (note ways you did so in your Collaboration section) and to use comments in the document to indicate things you tried but what went wrong/where you got stuck.
Remember that you need to submit your lab separately from your partner.
Extensions
- Find values of C and n0 that demonstrate the big-O notation for the earlier exercises.