Nested Loops Lab
This is a lab assignment and so you will not be submitting it. However, the concepts and practice will help you on both the homework and quizzes so I encourage you to make a serious effort on it during class and consider finishing it outside of class.
I recommend making a folder for today’s lab in COURSES as you usually do.
Exercise 1
Think about what the output of each of these snippets will be and then test them. Feel free to put them into PythonTutor to help with tracing through them.
# Snippet 1
n = 4
m = 3
for i in range(n):
for j in range(m):
print('*', end='')
print()
# Snippet 2
n = 4
for i in range(n):
for j in range(i+1):
print('*', end='')
print()
# Snippet 3
n = 4
for i in range(n):
for j in range(i):
print('-', end='')
for j in range(i, n+i):
print(j, end='')
print()
# Snippet 4
n = 4
for i in range(0,n):
for j in range(0,n-i-1):
print(' ', end='')
for j in range(n-i-1,n):
print('*', end='')
print()
# Snippet 5
n = 4
for i in range(0,n):
for j in range(0,n-i-1):
print(' ', end='')
for j in range(n-i-1,n+i):
print('*', end='')
print()
# Snippet 6
n = 4
for i in range(n):
for j in range(0,-1*n,-1):
for k in range(2):
print(j*k, end='*')
print(i, end=' ')
print()
Exercise 2
Revisit the reverse word problem now that you know how to use nested loops.
- Get phrase from user.
- Split phrase into words
- For each word in the phrase
- Reverse the letters
- Combine the letters back together
- Print the reversed word
Exercise 3
Consider the following code (with blanks that you will fill in):
ranks = ['Two', 'Three', 'Four', 'Five', 'Six', 'Seven', 'Eight', 'Nine', 'Ten', 'Jack', 'Queen', 'King', 'Ace']
suits = ['Clubs', 'Diamonds', 'Hearts', 'Spades']
deck = []
for _________________:
for _________________:
#f"{x}" is another way of doing the format function
deck.append(f"{rank} of {suit}")
for card in deck:
print(card)
a. Fill in the blanks above such that the cards are printed out increasing by number (e.g., all of the twos, then all of the threes, then all of the fours, etc.) as below:
Two of Clubs
Two of Diamonds
Two of Hearts
Two of Spades
Three of Clubs
...
King of Spades
Ace of Clubs
Ace of Diamonds
Ace of Hearts
Ace of Spades
b. Fill in the blanks such that the cards are printed out by suit (i.e., all of the clubs, then all of the diamonds, then all of the hearts, then all of the spades), as below:
Two of Clubs
Three of Clubs
Four of Clubs
...
Ace of Clubs
Two of Diamonds
Three of Diamonds
...
King of Spades
Ace of Spades
Exericse 4
Write a nested for-loop that creates the following output:
0 x 0 = 0 0 x 1 = 0 0 x 2 = 0 0 x 3 = 0
1 x 0 = 0 1 x 1 = 1 1 x 2 = 2 1 x 3 = 3
2 x 0 = 0 2 x 1 = 2 2 x 2 = 4 2 x 3 = 6
3 x 0 = 0 3 x 1 = 3 3 x 2 = 6 3 x 3 = 9
Exercise 5
There are many ways of encoding or encrypting messages by changing the letters into numbers or other letters.
One common encryption algorithm is ROT-13. It derives its name from the fact that it rotates each letter in a message 13 places forward in the alphabet, rotating around to the beginning if necessary. So, for instance, the letter “A”, which is 1st in the alphabet, will become the letter “N”, which is 14th in the alphabet. “C” (3rd) becomes “P” (16th). “R” is the 18th letter in the alphabet. 18 + 13 = 31, which is more letters than we have–so once we go off the end, we start at the beginning with “A”, which means that “R” will become “E” (5th).
There are a couple of advantages of this algorithm:
- Encrypting messages is easy! Just add 13 to each letter. (Though be careful about going off the edge… seem like a good use of modular arithmetic?)
- Decrypting messages is just as easy! In fact, because there are 26 letters in the alphabet, we decrypt messages using the same algorithm as decrypting them!
Take a minute to practice by decrypting this secret message:
PF VF NJRFBZR
Once you feel confident in how the algorithm works, write up a Python program that will decrypt a ROT-13 string given by a user. In pseudocode, your algorithm should look something like this:
- Get a string from the user (using input())
- For each letter in the string:
- Print out the letter 13 places back in the alphabet–being careful to wrap around to the end if necessary.
Some notes:
- You can assume the message is entirely in lowercase.
- Digits, spaces, and punctuation should be printed out as they are, without being rotated at all.
- The
ord()function converts characters into their ASCII value (e.g.,ord("a")will return 97,ord("z")will return 122).Here is an ASCII reference table
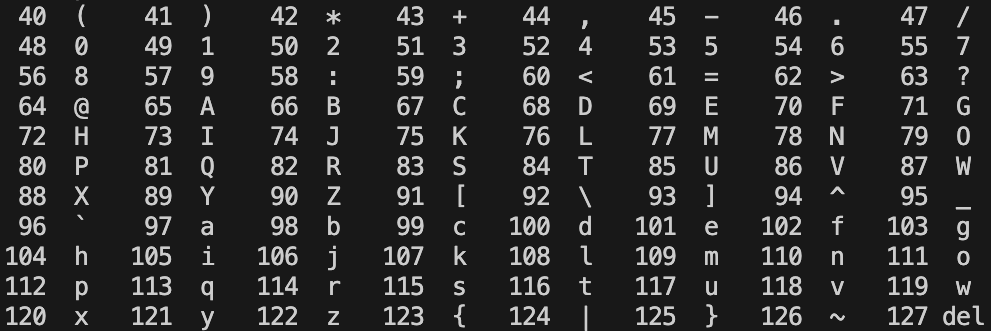
- The
chr()function goes in the opposite direction, converting an ASCII value to a string (e.g.,chr(97)returns “a”,chr(122)returns “z”). - You may also find this list of Python string methods helpful for reference and section 9.9 of your textbook
Exercise 6
Write another Python program that will encrypt a message for a user, so it will move every letter forward in the alphabet by 13.
Exercise 7
By this point, you have likely surmised that ROT-13 isn’t a very secure method of encryption. One way we could improve it a bit would be to generalize it away from the number 13, allowing users to use any agreed upon number from 1-26. (This generalization is sometimes called the Caesar cipher.)
Extend your program from Exercise 5 to take both a message and a rotation (an integer between -26 and 26) and then apply the rotation to the message. Be careful to check for the need to rotate around to the other side in both directions.
Extra
Note: this part is much harder, but hopefully a fun extension!
Your solution to Exercise 6 is a bit better, but still not quite secure. For one thing, we’re assuming that we have a secure channel across which two people can tell each other what rotation to use. If they can communicate that… why not just communicate their message?
But maybe they shared the rotation in person and no one had the chance to overhear it. How, then, might an eavesdropper still decipher their message?
Write a program that takes as input a message that has been encoded using a Caesar cipher (with an unknown rotation) and helps you determine what the original message was. This part is intentionally more open-ended than the previous two. I would suggest first writing a program that might also require some intuition on the part of the user (“Here is a list of things the original message might be…”) and then potentially modify that program to make some informed suggestions about which rotations are most likely to have been the original one.
Some things that you might consider:
- Here are the frequency of letters in the English language, how could you count the most frequent letter in the input and use that information to help you?
- Also potentially useful could be the most common words in the English language
There are many ways to approach this problem, and many of those are likely to take much longer than the class period. Brainstorming some pseudocode approaches is a good starting point!
Acknowledgements
This lab is based on labs from Profs. Eric Alexander and James Ryan.